

 For this to work, they needed an approximation
of pi, calculating procedures, and accurate construction methods6.
For this to work, they needed an approximation
of pi, calculating procedures, and accurate construction methods6.
Sulva means "cord", and the sulva-sutras are so named because the Hindu priests used a simple cord or string for all (or at least most) of their constructions. This cord could work as a straight edge (stretched tight), a compass (drawn around a point), and more (such as getting proportional lengths, by doubling the string over itself the desired number of times). A pole was also often used, for functions such as the making of circles and also sometimes in marking corners of rectangles, so that the cord could be stretched around the poles to make various measurements7.
The sulva-sutras begin by giving the names and measures of the units that will be used. To give you an idea of the kind of units that were used: "The following is the measure of an Angula: Fourteen grains of the anu-plant."8 Then, they go on to give the rules for various "constructions" which will be used later on to build the actual altars. These constructions are what give us most of our information about the Hindus' mathematical knowledge.
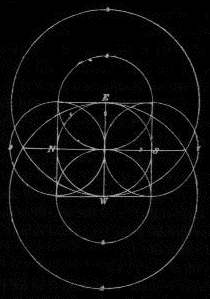
One striking discovery is that there were many examples included of the wrongly named "Pythagorean theorem", or the rule for the lengths of sides of right triangles (now written as a2+b2=c2). It was expressed as "the cord stretched in the diagonal of a rectangle produces both areas which the cords forming the longer and the shorter side of a rectangle produce separately."9 In other words, the sum of the squares of the two different sides of the rectangle equals the square of its diagonal. ("Squares" probably meant the area of actual squares drawn on the three sides of the triangle formed.) "Pythagorean triplets", sets of side lengths that can be expressed as integers (for example 3,4,5 and 5,12,13), were used as a sort of proof of that proposition, and were also used to make right angles. One problem which the priests must have run into was that they could not find any squares with the sides and diagonal of integral lengths.10 In the end, they came up with an incredibly close approximation (6 digits of accuracy) to the square root of 2 (the length of the diagonal of a square whose sides are one unit).

|
Another of their most famous problems is that of getting a square and circle to be equal in area. Two authors used very different constructions (neither of which actually uses pi) which both lead to a value of pi very close to 3.08831 (pi is actually about 3.14159). What's remarkable is the similarity of the two values, but one must wonder how this particular value was reached. (It might be noted that only one of the authors showed knowledge that his method was an approximation.)11 |
Along with the "simple" mathematics involved in altar-building, there were very complicated problems to decide what math to use where. One of these problems can be understood just by the fact that the most basic altar was in the form of a falcon! However, all of the bricks retained a square, rectangular, triangular, or circular shape. So the precise dimensions and area of every brick had to be calculated, after the specific design was decided upon. Usually, the total area was 7-1/2 units, because that was convenient for the falcon shape. But to make matters exponentially "worse", when two or more altars were made for the same purpose, subsequent ones usually had to be one unit bigger than the last; and the areas of each brick had to stay proportional.12 As you can infer, this was one heck of a math problem! And it had to be done twice for each altar, because a different design was needed for alternating layers, so that spaces between bricks weren't directly over each other.13 |
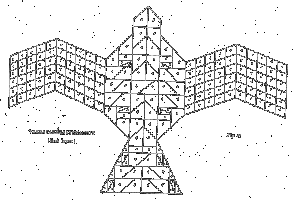 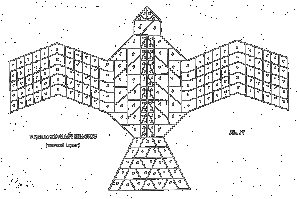
|
It doesn't take a genius to understand that most of the Latin words were obviously derived from those of Sanskrit. And the fact that the names of the numbers were copied into Latin (and then other languages) very heavily suggests that the ideas of the numbers were transferred as well. Even the order of "digits" remains the same from Sanskrit to Latin. And simply the fact that the decimal system remains in use heavily testifies to the Indian origin.
The other concept which Mr. Pandit thinks originated in India is that of zero. Firstly, the name for "zero" in Sanskrit is sunya. The Arab word is assifr, then sifra, the Latin word is cifra, and then the Italian words are zefiro, zefro, and then zevero -- which leads to the English zero.15 This is somewhat of a long stretch in my opinion, but it does deserve merit. Looking back at the table, another thing that comes to mind is the fact that the symbol for "ten" isn't a compound word in any of the languages. This is further similarity between the languages, and it also brings up another point in Indian mathematics -- the positional system. Although we think of this as positions of powers of ten, the single dasa (ten) indicates that the ancient Indians probably thought of it more as multiple "number-series".16 In other words, 43 would mean "the third number in the fourth series of tens." So when you just have 10, it would just be "the 1st series of tens", or "ten" or dasa. The zero in the "ones place" is either not represented, or represented by nothing. In any case, Mr. Pandit firmly believes that "the concept of 'the zero or sunya' definitely originated in the Vedas... And it must be said that it is from and in Vedic mathematics that the zero is born. And it is from the Vedas that all other civilizations have borrowed the concept and device of positional notation of numbers and consequently of zero."17
The final topic which I wish to discuss is the way Indian mathematics differ from that of the Greeks and Romans (the civilizations that are given the most attention mathematically). In India, mathematics was developed to aid in rituals to please the gods. Most probably, the originators of math in both the Vedas and the Sulva-sutras were priests. This contrasts sharply with the philosophers of Greece and Rome, proving every theorem and analyzing every math form. The Vedas and Sulva-sutras were not concerned with proofs or reasons, only with the correct performance of rituals so that their crops would grow. This may seem primitive or even inferior18, but (1.) the Indians produced an amazing amount of mathematics, many of which are still in use today, and (2.) their rules are still correct. What more could you ask for?

7 Thibaut, George. Mathematics in the Making in Ancient India. Calcutta: K.P. Bagchi, 1984. [bibliography entry]
8 George Thibaut, trans., Baudhayana Sulva-sutra, "Adhyaya I". p 69 in Mathematics in the Making in Ancient India. [bibliography entry]
9 Baudhayana 74. [bibliography entry]
15 Menninger, Karl. [bibliography entry]
Number-words and Number-Symbols. trans. Paul Broneer. London: MIT, 1969, p 401.
18 As Morris Kline thinks in his Mathematical Thought from Ancient to Modern Times, New York: Oxford University Press, 1990, p 183. [bibliography entry]